October 2022

I am elated to report the acceptance of my recent work at the IET Generation, Transmission & Distribution (GTD) open access (OA) journal of the Wiley publications! Before unpacking my paper with the (kind of long) title “Stochasticity Agnostic Solution to the AC Optimal Power Flow by Recursive Bound Tightening with Top-Down Heuristically Inducted Binary Decision Trees” (link here), let me rejoice in the fact that the IET GTD is, according to Scholar Google, the highest ranking Q1 (in Control & Systems Eng., Electrical & Electronic Eng., Energy Eng. & Power Technology) OA journal on Power Engineering. I have been an avid proponent of OA and Associate and Senior Editor in 2 such publications. Going through the process as an Author myself has reassured me that my heart is in the right place with OA! Read more about my position on OA here.
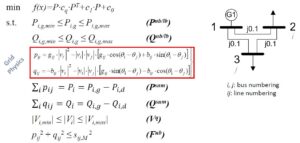
The AC Optimal Power Flow (OPF) is a non-convex optimization problem for resources or performance metrics within an electrical grid (see formulation above). The non-convexity of the AC OPF is due to the grid physics of power flows that introduce a non-convex equality constraint to the optimization formulation. Since the AC OPF per se is – almost – never the end-problem we wish to solve, the sizes of problems encapsulating AC OPF are typically orders of magnitude larger than that and may include additional non-convexities, e.g. integer variables. The most typical approach used by several researchers in the recent years is the convex relaxation of the AC OPF to a larger dimension and – provided some conditions are met – projection of the relaxed solution back to the feasible space of the original AC OPF problem. Much fewer approaches have considered machine learning for solving the AC OPF and even fewer of those come with guarantees of global optimality. The overall framework here described clearly means that the AC OPF cannot be solved in times that make sense for system operators and other electricity stakeholders when making decisions about how to operate and plan the electrical grid functions.
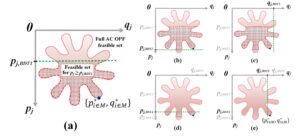
My paper introduces 2 perspectives to solving the AC OPF per se and another 1 in accounting for volatile resources, such as renewables like wind generators and photovoltaics. But first of all, let me describe in a few words how the solver works (assuming we wish to minimize an objective function of energy cost). It starts by sampling the whole feasible space of the AC OPF instance. The samples are, essentially, random feasible dispatches for said problem. Then the method labels half of the samples as False, if the objective function is greater than the median cost of the samples, and True otherwise. Then a heuristically inducted binary decision tree (BDT) is trained with these samples and tightens/shrinks the feasible space (clearly towards the region of the feasible space with costs below the noted median). The method is recursively employed until the feasible space has tightened/shrunk around the global optimum (see “tightening” steps (a)-(e) in the the graph above).
Solving the AC OPF – Point 1
I prove that the method converges to the global optimum via Bayesian inference. Most typically, AC OPF solvers (and relaxations building upon them) pursue to solve the dual problem, relying on strong duality conditions that indicate that the solution of the primal and the dual problems are the same. I take a different path… I prove that a Bayes classifier for the global minimum in a small vicinity around it exists. This is true, due to the fact that the feasible space has non-random characteristics and I also explicitly label the global optimum (and some epsilon around it) as such, while the rest of the said vicinity as non-globally-optimum. From that point, iteratively, I can expand to the whole feasible space by properly labeling/splitting the vicinities of the feasible space as optimal/sub-optimal.
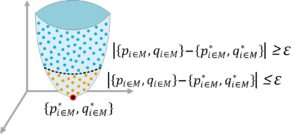
The existence of these Bayes classifiers means also the existence of the heuristically inducted top-down binary decision trees (BDTs) for the same classifications of optima/non-optima. The second part of the proof here could not have been possible if it had not been for Guy Blanc‘s, Jane Lange‘s & Li-Yang Tan‘s recent work on heuristically inducted BDTs. In 2020, Guy et al proved that if there exists a minimum (in the sense BDT-size; nothing to do with the underlying optimization problem here) classifier for a given function, then there exists a non-optimally-sized BDT for that same function. I am pointing this out, because the first time I have used a draft/reduced version of this method (back in 2010), I could not explain why/how the BDT would consistently converge to an optimum… Well, now I know – thanks Guy, Jane and Li-Yang!
Solving the AC OPF – Point 2
Even though it kind of stems from Point 1, it is a remark that I wish to separately mention here. The steps of tightening the AC OPF feasible space towards the global optimum seem unaffected by the size of the grid, but follow the number of the decision variables. In the way I have structured the solver, the decision variables are the active and reactive power set-points of the generating resources. This can be particularly valuable when larger grids with fewer resources must be optimized. Given how typical solvers descend along gradients of a feasible space, the size of the latter will affect that descent. Hence, larger grids, meaning greater numbers of voltage angles, magnitudes and flows, will be slowing down the solving descent. In the AC OPF solution I propose, the size of the grid does not matter, provided that the BDT training samples are feasible and adequate. This is particularly interesting, because we can consider how to accelerate this solution via the control intervals of generators, which are typically not continuous and cannot take any value between minimum and maximum (looking for the exact NERC rule and I will cite it here).
Effect of Volatile Resources in Solving the AC OPF
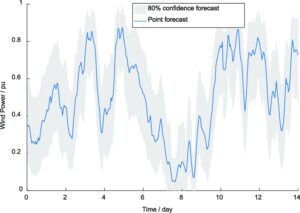
Typically, renewable energy has negligible, if not zero, operating costs, hence, gets dispatched by priority in any electricity market. However, the exact amount of available renewable energy is usually impossible to determine ahead of time and only offered within some forecasted confidence intervals (see forecasting figure below). This means that as the proposed AC OPF solver converges to the global optimum by the successive median cost of the sampled feasible space, the commitment of renewable energy within the AC OPF increases towards the global optimum at a decreasing confidence. In other words, renewable energy will be committed within the AC OPF at lower set-points corresponding to higher forecasting confidence in the first few iterations of the method (higher objective function costs) and at higher set-points of limited confidence when the process converges to global minimum.
As in my last paper, I had the joy to work with another CMU MSc student, who put in some coding work for me; Parth joined me along for the ride on the paper authorship, too! It was fun and very rewarding to substantially advance my past work on machine-learning-driven optimization of electrical grids with volatile renewables, gain better understanding of the methodology and its characteristics, test it rigorously for performance and get it published OA. Next steps are determining appropriate BDT training sizes and focusing on the stochasticity aspect of this AC OPF solver. Feel free to reach out for any ideas for extensions or collaborations; I will be glad to see more applications of this tool!